Physics-Inspired Temporal Learning of Quadrotor Dynamics for Accurate Model Predictive Trajectory Tracking
Alessandro Saviolo, Guanrui Li, Giuseppe Loianno

Abstract. Accurately modeling quadrotor's system dynamics is critical for guaranteeing agile, safe, and stable navigation. The model needs to capture the system behavior in multiple flight regimes and operating conditions, including those producing highly nonlinear effects such as aerodynamic forces and torques, rotor interactions, or possible system configuration modifications. Classical approaches rely on handcrafted models and struggle to generalize and scale to capture these effects. In this paper, we present a novel Physics-Inspired Temporal Convolutional Network (PI-TCN) approach to learning quadrotor's system dynamics purely from robot experience. Our approach combines the expressive power of sparse temporal convolutions and dense feed-forward connections to make accurate system predictions. In addition, physics constraints are embedded in the training process to facilitate the network's generalization capabilities to data outside the training distribution. Finally, we design a model predictive control approach that incorporates the learned dynamics for accurate closed-loop trajectory tracking fully exploiting the learned model predictions in a receding horizon fashion. Experimental results demonstrate that our approach accurately extracts the structure of the quadrotor's dynamics from data, capturing effects that would remain hidden to classical approaches. To the best of our knowledge, this is the first time physics-inspired deep learning is successfully applied to temporal convolutional networks and to the system identification task, while concurrently enabling predictive control.

Introduction
Unmanned aerial vehicles (UAVs), such as quadrotors, have become important platforms to help humans solve a wide range of time-sensitive problems including logistics, search and rescue for post-disaster response, and more recently reconnaissance and monitoring during the COVID-19 pandemic. These tasks often require robots to make fast decisions and agile maneuvers in uncertain, cluttered, and dynamic environments. In these scenarios, to safely control a UAV, it is critical to accurately model the system dynamics to capture the highly nonlinear effects generated by aerodynamic forces and torques, propellers interactions, vibrations, and other phenomena. However, such effects cannot be easily measured or modeled, thus remain hidden. Moreover, for some UAV applications, the platform may be extended with external payloads that would significantly change the dynamics by varying the mass and moment of inertia. Overall, failing to model such system changes would result in significant degradation of the flight performance and may cause catastrophic failures.
Related Work. Classic modeling of the quadrotor's dynamics is performed using physics-based principles approaches which result in nonlinear ordinary differential equations. However, these nominal models only approximate the actual system dynamics and do not take into account external effects caused by aggressive maneuvers or system modifications. To circumvent this issue, recent works have investigated data-driven approaches for modeling system dynamics. Several methodologies exist, from combining nominal models with learned residual terms to fully predicting the system dynamics using neural networks.
Contributions.
We design and present PI-TCN for learning quadrotor dynamics. To date, this is the first time physics-inspired learning is applied to temporal convolutional networks since most of the approaches have only focused on feed-forward and recurrent neural networks;
We perform an extensive evaluation by comparing the predictive performance of the proposed methodology against nominal, residual, and learning methods on unseen test maneuvers in both simulation and real-world settings. We experimentally validate the network's design choices and propose several ablation studies to evaluate their roles in capturing quadrotor's dynamics from data, even highly nonlinear effects that remain hidden to classical and residual approaches;
We propose a model predictive control framework that leverages the learned dynamical model and we extensively test it to track multiple aggressive maneuvers.
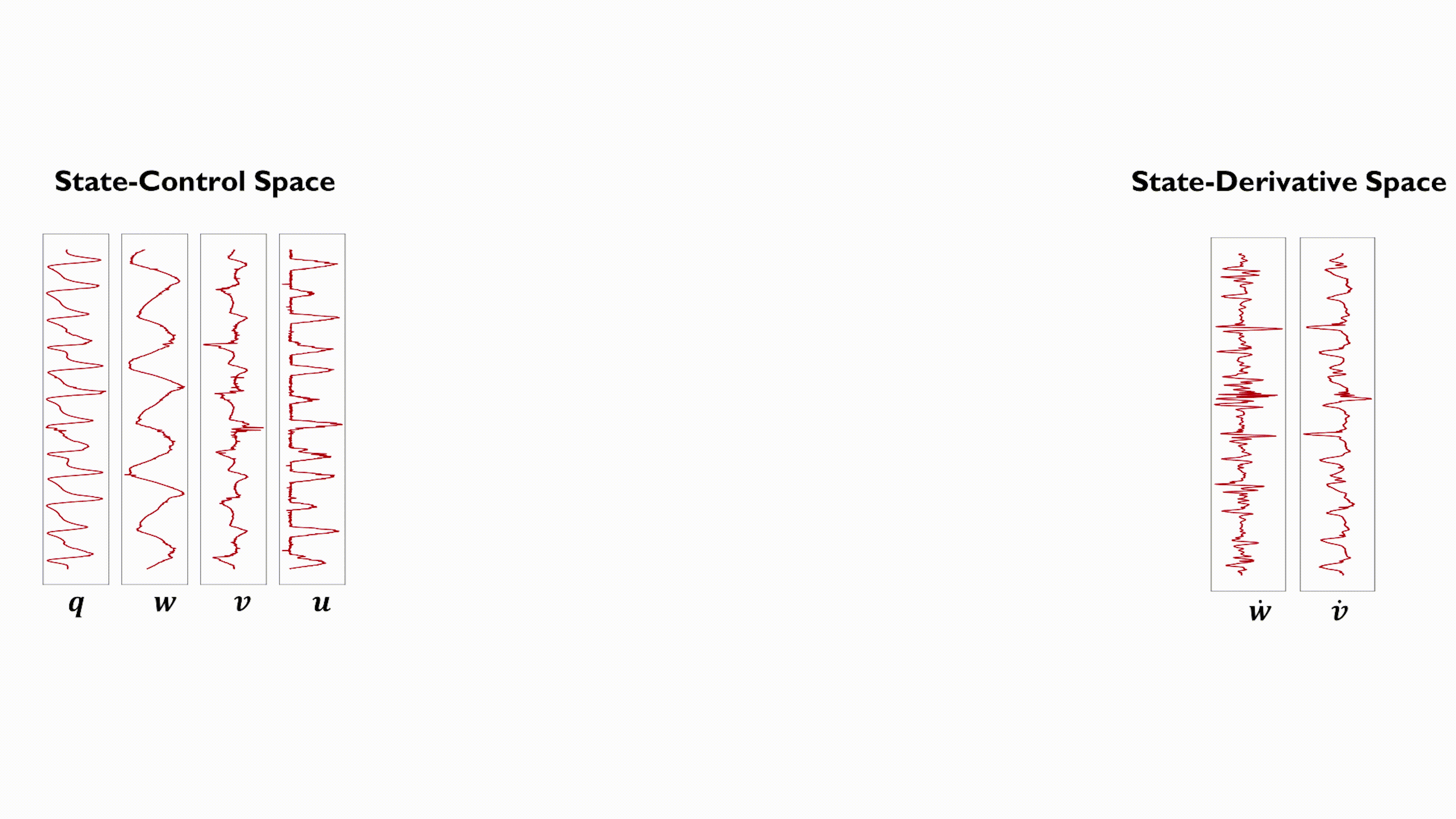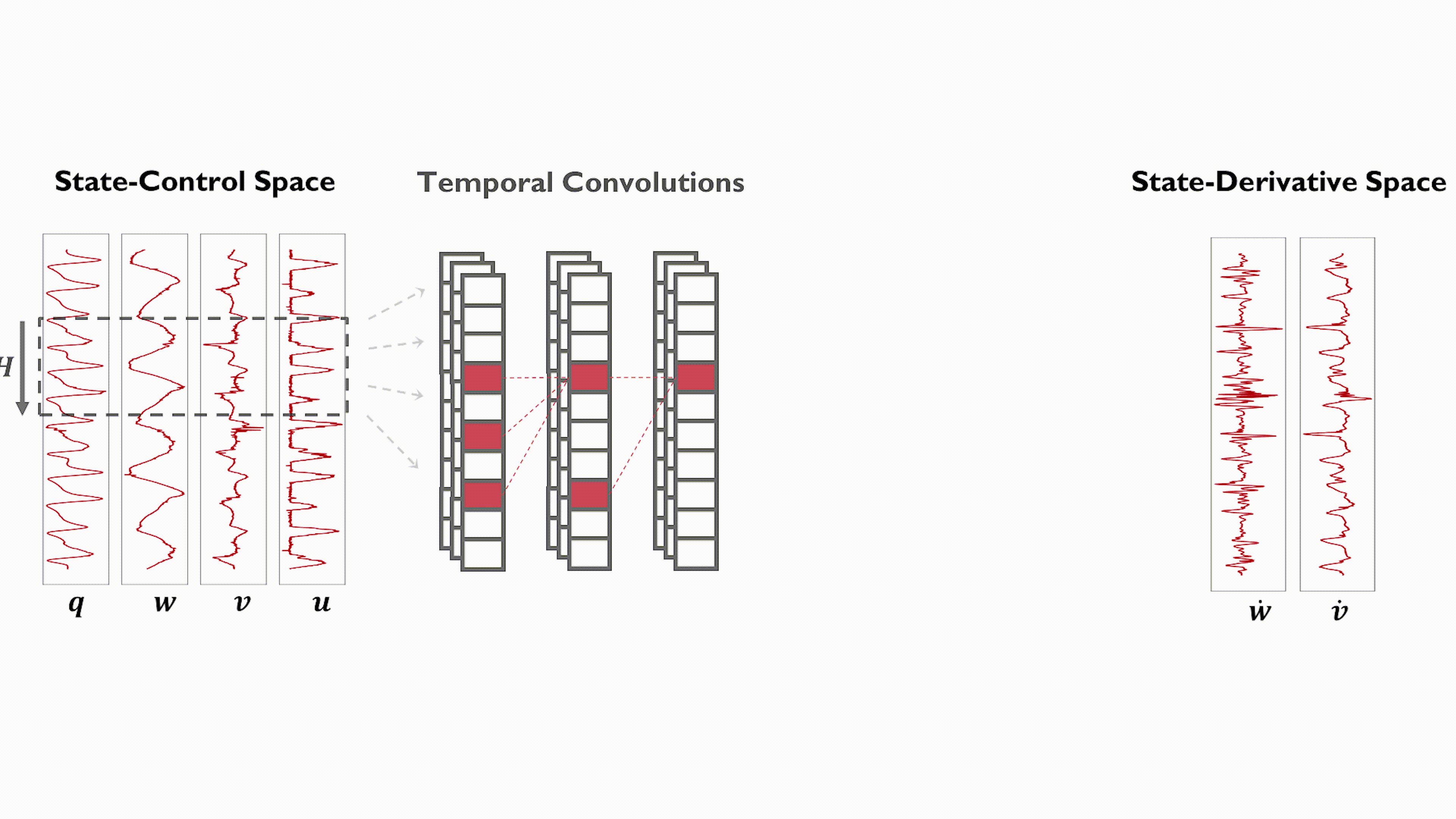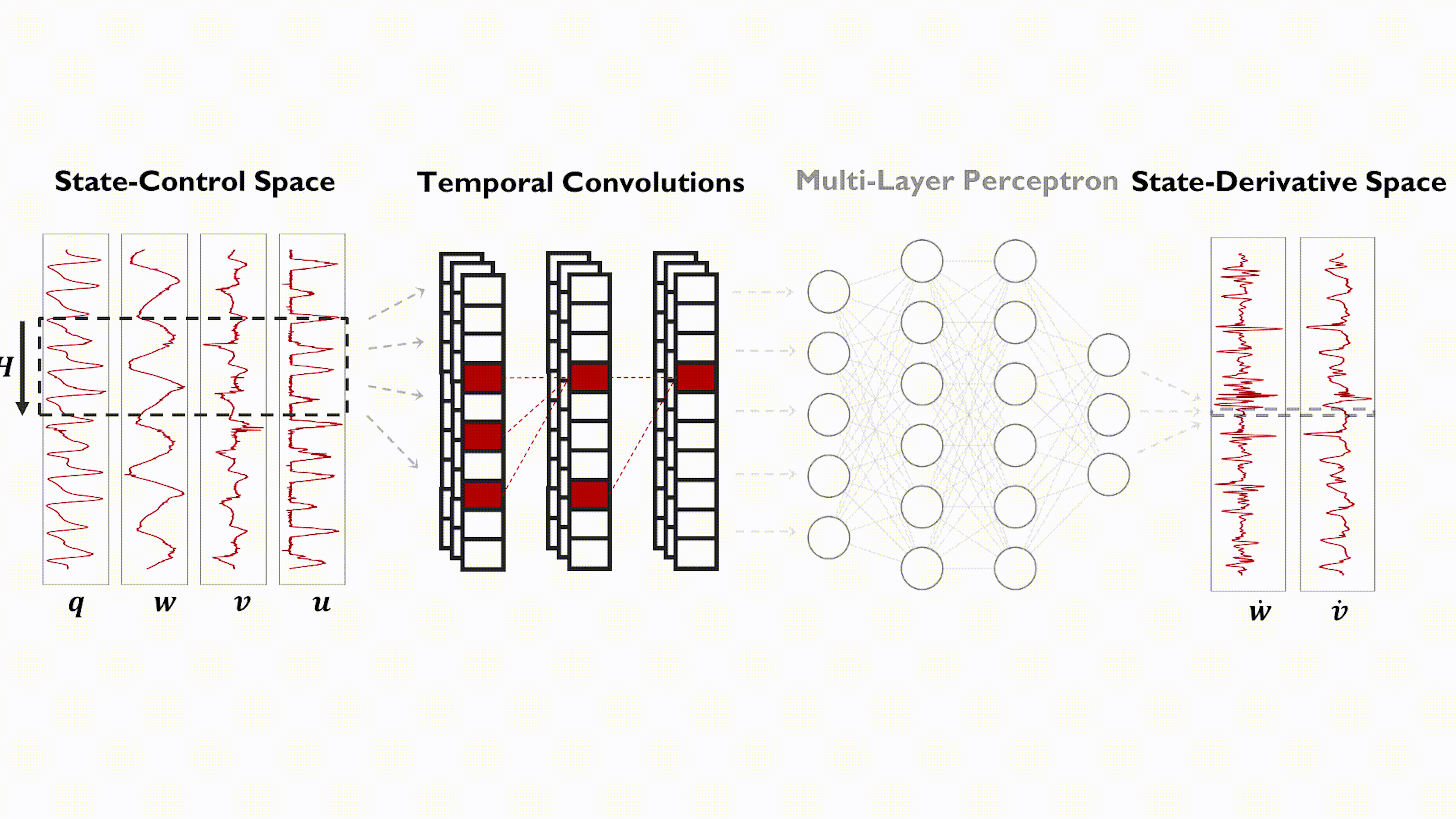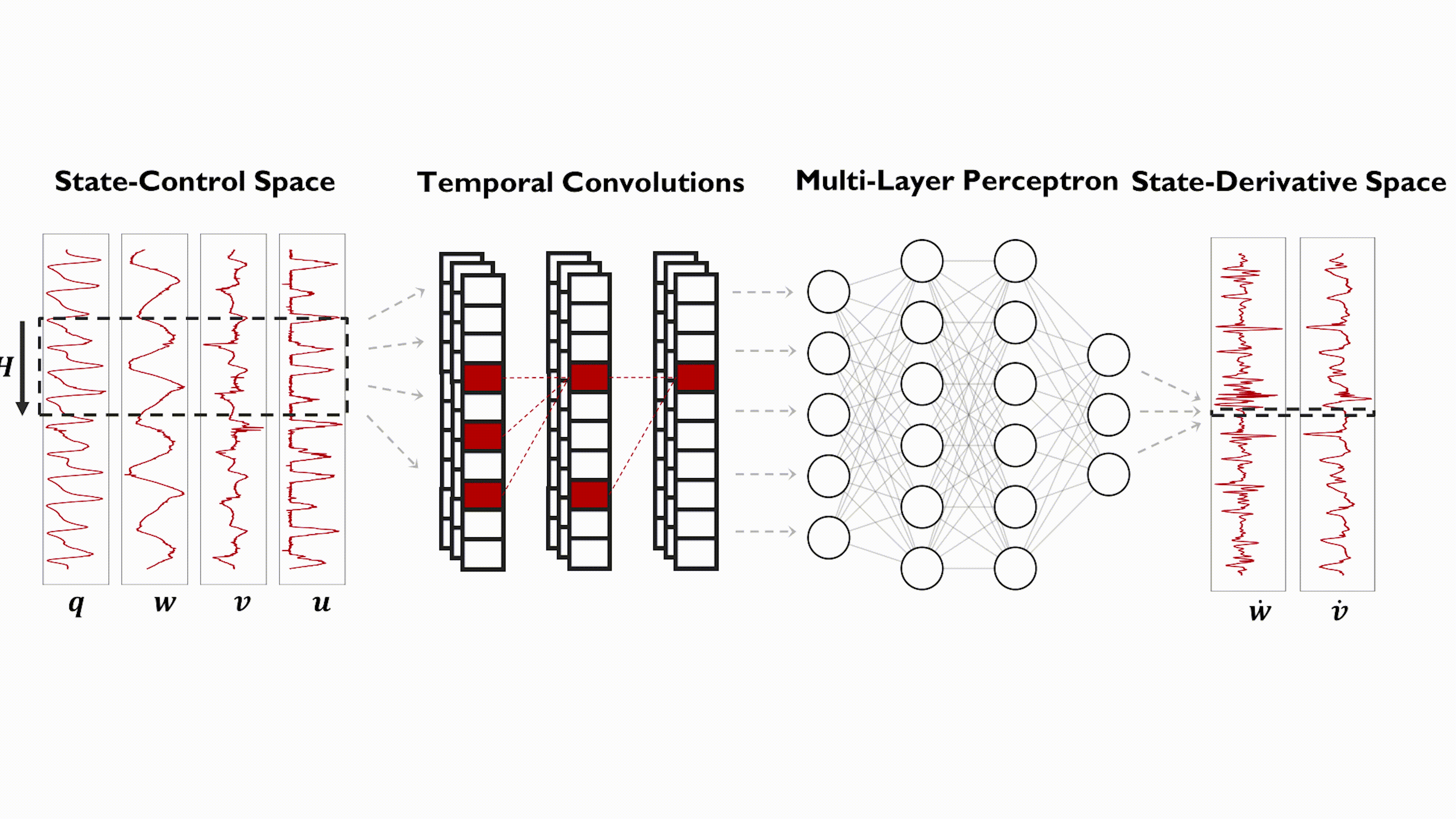
Method
Model Learning. In this work, we model the quadrotor's system dynamics using a physics-inspired temporal convolutional network and leverage past flight states and control inputs to predict the quadrotor's full dynamic state. The proposed network, illustrated in Figure 3, consists of two sub-networks, a temporal convolutional network (TCN) and a multi-layer perceptron (MLP). The TCN extracts time-correlated features from a sequence of past flight states and control inputs and outputs a compact hidden-state vector. Such hidden state is passed in input to the MLP which predicts the quadrotor's full system dynamics. Such encoder-decoder architecture fully leverages the qualities of the TCN and MLP models. TCNs are sparse networks defined by dilated (causal) convolutional layers, which allow to process long history sequences in parallel while encoding the temporal structure of the input time series in their output feature vector. Conversely, MLPs are dense networks, which makes them better suited for making predictions from a compact hidden state representation.
Physics-Inspired Loss. Learning the dynamics purely from data poses the challenge to make the network generalizable outside the training distribution. However, it is necessary to concurrently guarantee that the network matches physical principles. Motivated by this observation, we embed physics constraints in the training process by including the physics laws in the loss function.
Experiments
Closed-Loop Tracking Performance. We validate the learned dynamical model against the nominal model in the real-world setting. Specifically, we employ the proposed MPC to control our quadrotor to track multiple trajectories with different models. We compare the tracking performance based on the positional RMSE. Figure 4 shows the results of this experiment.
Discussion and Conclusions
In this work, we proposed PI-TCN, a deep neural network that extracts quadrotor's dynamics purely from data by leveraging the expressive power of temporal convolutional networks and the generalizability offered by instilling physics laws in the training process. Furthermore, we showed how to exploit the network's predictive performances for accurate predictive trajectory tracking. The proposed learning method provides several demonstrated advantages over existing methods in the literature. While classic approaches only rely on present information to estimate the system's dynamics, PI-TCN takes advantage of a history of states and control inputs to capture time-dependent features that would otherwise remain hidden. Moreover, extending the present with past information makes the model less subject to noise in the data. We demonstrated these capabilities in several experiments where PI-TCN performs accurate predictions both in simulation and real-world settings, consistently outperforming the classical nominal model and the learning-based baselines. While other learning-based methods decouple linear and angular accelerations or only estimate the former, jointly learning linear and angular accelerations allows capturing the hidden dependencies that bound forces and torques for nonholonomic and underactuated systems like the quadrotor. This advantage is also empirically demonstrated by embedding the learned-based model in an MPC framework and accurately tracking trajectories in different flight regimes. One limitation of the proposed approach is the computational time required by the MPC to solve its online optimization problem. Future works will improve the efficiency of our implementation and leverage GPU parallel computation to fully exploit PI-TCN in the controller horizon.
