AutoTune: Controller Tuning for High-Speed Flight
Antonio Loquercio*, Alessandro Saviolo*, Davide Scaramuzza

Abstract. Due to noisy actuation and external disturbances, tuning controllers for high-speed flight is very challenging. In this paper, we ask the following questions: How sensitive are controllers to tuning when tracking high-speed maneuvers? What algorithms can we use to automatically tune them? To answer the first question, we study the relationship between parameters and performance and find out that the faster the maneuver, the more sensitive a controller becomes to its parameters. To answer the second question, we review existing methods for controller tuning and discover that prior works often perform poorly on the task of high-speed flight. Therefore, we propose AutoTune, a sampling-based tuning algorithm specifically tailored to high-speed flight. In contrast to previous work, our algorithm does not assume any prior knowledge of the drone or its optimization function and can deal with the multi-modal characteristics of the parameters' optimization space. We thoroughly evaluate AutoTune both in simulation and in the physical world. In our experiments, we outperform existing tuning algorithms by up to 90 % in trajectory completion. The resulting controllers are tested in the AirSim Game of Drones competition, where we outperform the winner by up to 25% in lap-time. Finally, we validate AutoTune in real-world flights in one of the world’s largest motion-capture systems. In these experiments, we outperform human experts on the task of parameter tuning for trajectory tracking, achieving flight speeds over 50 km/h.

Introduction
Flying high-speed trajectories with a quadrotor requires the platform's controller to be tuned meticulously. The complex relationship between parameters and performance is caused by unavoidable factors such as noisy actuation, imperfect modeling, and external disturbances. The higher the speed, the more complex the relationship between controller parameters and final performance is. This behavior is empirically shown by Figure 2.
Challenges. (i) The objective function (i.e. relationship between controller parameters and performance) is highly non-convex; (ii) The tuning process only relies on noisy evaluations of the objective function at adaptively chosen parameters, but not to the function itself or its gradients; (iii) Different parts of the trajectory, e.g. a sharp turn or a straight-line acceleration, generally require different controller behaviors, hence dynamically changing parameters.
Related Work. The traditional approach for automatic tuning and adaptive control, generally known as the MIT rule, requires the expression of the desired performance metric, e.g. the average tracking error over the entire maneuver, as a quadratic function of controller parameters, and then optimizes the controller with gradient-based optimization. However, expressing the long-term performance on a high-speed maneuver concerning the parameters of a receding horizon controller is generally intractable. Indeed, it requires to know a priori the exact model of the quadrotor and the disturbances acting on it during flight, e.g. noisy actuation and aerodynamic effects. Instead of analytically computing it, another line of work proposes to iteratively estimate the optimization function, and use the estimate to find optimal parameters. However, these methods make over-simplifying assumptions on the objective function, e.g. convexity or relative Gaussianity between observations. Such assumptions are generally not suited for controller tuning to high-speed flight, where the function is highly non-convex. To remove any assumption, model-free methods propose to directly search for optimal parameters using sampling. Such methods are however built on heuristics not necessarily suited to high-speed flight and generally require thousands of iterations to converge.
Contributions.
- We present a novel sampling-based method for tuning quadrotor controllers on the task of high-speed flight;
- We show that our method outperforms existing methods for automatic controller tuning and enables quadrotors to fly time-optimal trajectories both in simulation and in the physical world in one of the world’s largest motion-capture systems;
- We provide interesting insights into the relationship between the parameters of a receding horizon controller and its flight performance on high-speed maneuvers.

Method
Metropolis-Hastings Sampling. In this work, we use the Metropolis-Hastings algorithm to find the parameters of a controller flying time-optimal trajectories. We continue the sampling procedure up to when we find a solution satisfying some user-defined performance metrics, e.g. tracking error or trajectory completion. When found, we re-evaluate the solution four times to account for the randomness of the simulation. We stop the optimization if no solution is found after 200 iterations.
Trajectory Segmentation. Complex high-speed trajectories require different controller behaviors along the track. We split the trajectory into multiple segments according to the height gradient of the reference. In each segment different parameters are assigned to the controller. To account for the strong correlations between segments and keep the optimization global over the trajectory, the controller parameters associated with each segment are updated jointly.
Sampler Initialization. The Metropolis-Hastings algorithm requires an initial parameter configuration to initialize the sampling. Instead of using a random initialization, we propose to use an informed guess. Specifically, we use a Gradient Boosting regressor with default parameters to predict initial controller parameters for each trajectory segment. The training data for this regressor are controller parameters found to be optimal on 5 training trajectories different in layout from the testing ones. A different regressor is trained for each type of trajectory segment. Five features including information about the reference trajectory are used for prediction: the number of points in the segment, the slope of the line connecting the first and last point of the segment, as well as their height difference, and the mean velocity and acceleration. These features have been selected with a cross-validation procedure.
Experiments
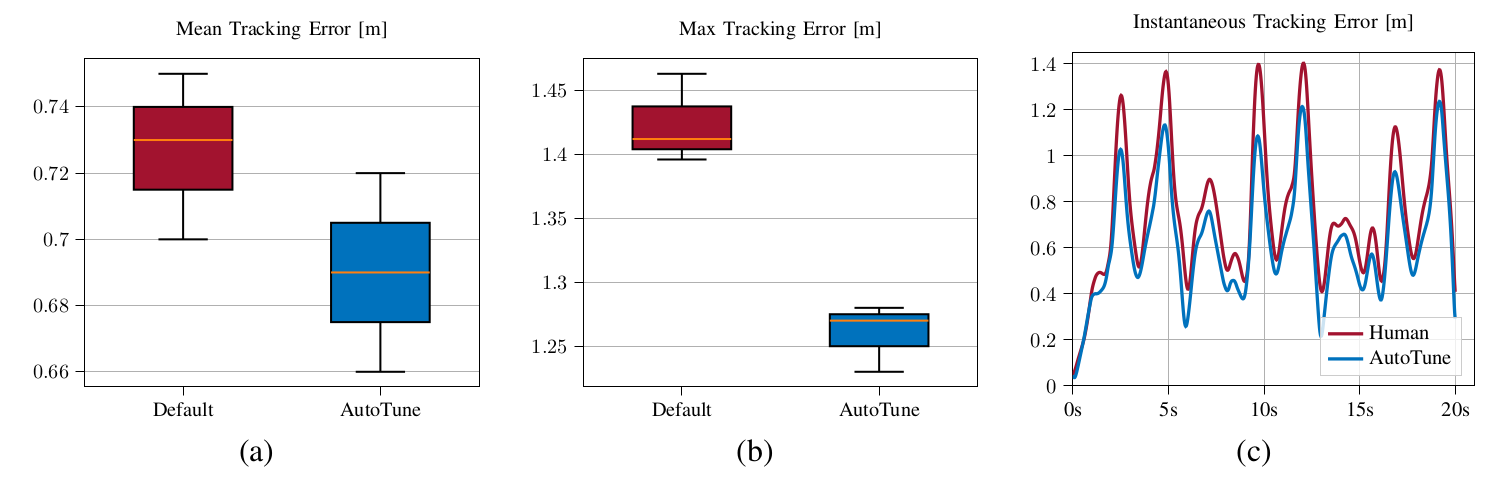
Tracking Minimum-Time Trajectories. AutoTune can be used to tune the controller of a physical platform. To do so, we compute a minimum-time trajectory double Split-S trajectory of 21 waypoints. This trajectory is used to tune the controller in the Flightmare simulator. The resulting controller is then evaluated on a physical platform in a tracking arena of volume 30x30x8 m, where the quadrotor achieves speeds over 50 km/h. Figure 5 shows the results of this experiment. AutoTune improves the average tracking error by 6 % and decreases the maximum displacement from the reference by 12 %. In addition, the controller parameters found by our approach give more consistent performance over multiple runs than the baseline.

AirSim Game of Drones Competition 2019. To validate the importance of tuning parameters for flying faster trajectories, we compare our approach to the top three methods in the 2019 AirSim Game of Drones competition. We compare the methods both on the qualification and final round of the competition. The results of this experiment are summarized in Figure 5. On the qualifier track flying AutoTune achieves a lap-time of 24.05 s, while the winner only reaches the goal in 30.11 s, with a lap-time 25 % longer than ours. Also in the final round, AutoTune outperforms the winner of the competition with a 1.7 s margin, completing the track in approximately 5 % less time. Interestingly, our approach converges to a policy with a maximum speed not necessarily higher than others. However, we achieve an average velocity higher than baselines, and therefore a faster lap-time. This experiment shows that tuning controller parameters with an automated procedure allow quadrotors to fly faster trajectories.


Discussion and Conclusions
This paper shows the importance of an automated tuning procedure of controller parameters to fly high-speed maneuvers. While the effect of tuning is less prominent at low speeds, it acquires a fundamental role when the quadrotor flies a minimum-time trajectory at the limits of handling. In such cases, the relation between the parameters of a finite-horizon controller and the flight performance over the entire trajectory (measured, for example, in terms of trajectory completion or tracking error) is non-convex, not injective, and multi-modal. In this paper, we propose a sampling-based approach specifically tailored to the task of high-speed flight. One limitation of the proposed approach is that it does not consider closed-loop stability during optimization. While prior work proposed a series of techniques to guarantee stability during tuning, such techniques either require a very accurate model of the platform or very conservative parameters exploration strategies. This makes them suited for tasks like hovering or low-speed flight but not to high-speed flight, where model mismatch makes the parameter's optimization landscape very complex. Similar to previous work on the agile flight, we have addressed this problem by tuning the controller exclusively in simulation and directly using the tuned controller on a physical platform. However, such a strategy strongly depends on the quality of the simulation environment. Therefore, combining existing techniques for safe tuning with our approach, to either tune from scratch or only finetune the controller on the physical platform, is a very exciting venue for future work.
